E-East-Northeast

题意

给定一个正整数集合 $S$，你要从 $\left(0,0\right)$ 走到 $\left(n,n\right)$。每次你可以将当前坐标 $\left(x,y\right)$ 变为 $\left(x+a,y+b\right)$，满足 $x+a\ge y+b,a,b\in\mathbb{N}^*,a\in S$，求方案数。答案对 $998244353$ 取模。

$n\le 2\times 10^5$

题解

首先对坐标的操作可以转化为，每次要么 $\left(x,y\right)\rightarrow \left(x+a,y+1\right)$，要么 $\left(x,y\right)\rightarrow \left(x,y+1\right)$。考虑这个过程倒过来。

将坐标变换转化为，有一个计数器，维护的是 $y-x$ 的值。初始时为 $0$，每次可以 $+1$，或者 $+1-a,a\in S$，要求任意时刻大于 $0$，求操作 $n$ 次后恰好为 $0$ 的方案数。

考虑往里面加一个额外的 $+1$ 操作，此时根据 Raney 引理，这个长度 $n+1$ 的操作序列只有一种循环同构是合法的，而这个循环同构的第一项一定是 $+1$，将其删掉则与原合法序列一一对应。

因此，答案即为

$$ \dfrac{1}{n+1}\left[x^n\right]\left(1+\sum_{i\in S}x^i\right)^{n+1} $$

复杂度 $\mathcal{O}\left(n\log n\right)$

F-Forbidden Pattern

题意

有一个 AB 构成的串 $S$，你每次可以选出 $S$ 的一个连续字串，满足其长度为 $2$ 且不为 AB，将其删除。求最后能得到多少种本质不同的串。

$\left|S\right|\le 10^6$

题解

先咕了

G-Git Gud

有一份包含没有优化过的并查集的程序，伪代码如下：

N = read_integer()

parent = array(N, -1) // 将这个序列初始化为 -1

find(v):
    if parent[v] == -1:
        return v
    else:
        return find(parent[v])

union(a,b):
    parent[find(b)] = find(a)

for i = 0 to N-2:
    A_i = read_integer()
    B_i = read_integer()
    union(A_i,B_i)

这个程序的输入为一棵树：

$N$

$A_0$ $B_0$

$A_1$ $B_1$

$\vdots$

$A_{N-2}$ $B_{N-2}$

现在，你希望把这个程序给卡飞，即，使得 find 被调用的次数尽可能的多。你可以任意排列 $\left(A_0,B_0\right),\left(A_1,B_1\right)\cdots \left(A_{N-2},B_{N-2}\right)$ 这 $N-1$ 条边的顺序，也可以调换任意一对 $A_i,B_i$ 的顺序，求 find 被调用次数的最大值。

题解

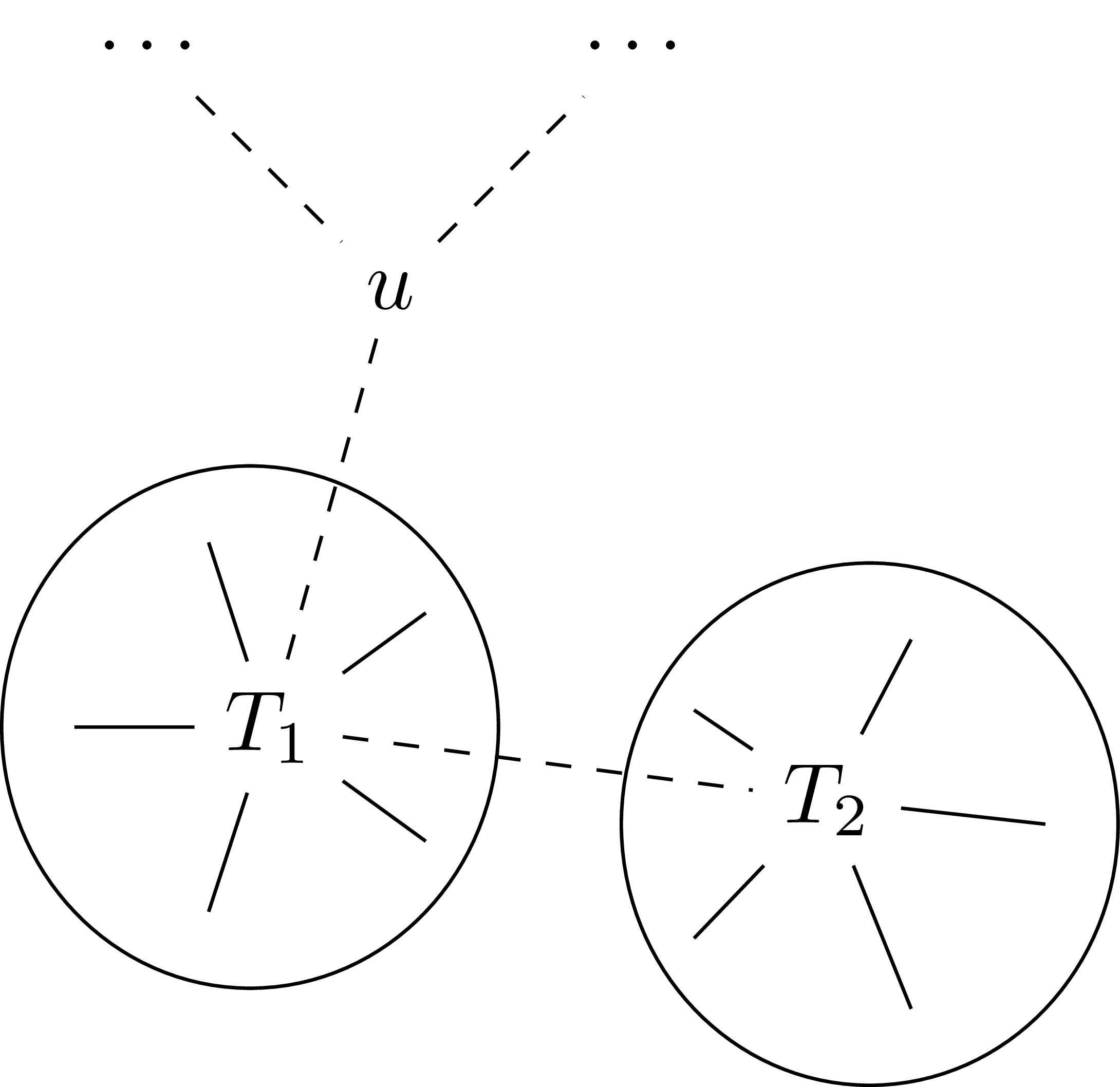
考虑最后建出来的 parent 树在原树中对应的边序列。

假设当前连通块是 $T$，对应的 parent 树的根是 $u$，$u$ 的儿子对应的子树为 $T_1,T_2,\cdots$。则 $T_i$ 一定是原树中的一个连通块。且 $\left\{u\right\}\cup T_i=T$，$T_i$ 和 $T_j$ 无交，$T_i$ 和 $\left\{u\right\}$ 也无交。

而不难发现，以上条件也是个充分条件。因为，通过以下伪代码构造，即可构造出合法的 parent 树。

solve(T):
    u=root(T) // u 为选定的根
    T1,T2,...=partition(T\{u}) // 将 T 去掉 u 后划分成若干个连通块。
    e1,e2,...=E-E(T1)-E(T2)...// 取出剩下的边。
    for Ti:
        solve(Ti) // 递归构造
    for ei in top(e) // 按照从 u 开始的 bfs 序遍历所有边。
        [x,y]=ei // x 为距离 u 较近的端点。
        merge(x,y) //将 y 的并查集的根的父亲设为 x 的并查集的父亲。
        // 由于是按 bfs 遍历的，因此每次遍历的时候，加入 parent 树的，一定一个端点是 u，一个端点是划分出来的 Ti 对应的 parent 树的根。

因此这是个充分必要条件。

用人话说，就是加强版建点分树，每次把当前连通块的根删掉，再删掉一些边，对每个连通块分别建立他们的点分树，最后再将那些子点分树的根作为当前连通块的根的儿子。