Project Euler 508 Integers in base i-1

题面

对于任意高斯整数 $a+bi\left(a,b\in \mathbb{Z}\right)$，定义它的 $i-1$ 表示法为 $01$ 序列 $d_0,d_1\cdots d_m$ 使得：

• $a+bi=\sum_{j=0}^md_j\left(i-1\right)^j$
• $d_m\neq 0$，除非 $a+bi=0$，此时令 $m=0,d_0=0$

可以证明对于任意高斯整数它的 $i-1$ 表示法是唯一的。

定义 $f\left(a+bi\right)=\sum_{j=0}^md_j$，令 $B\left(L\right)=\sum_{a=-L}^{L}\sum_{b=-L}^Lf\left(a+bi\right)$

求 $B\left(10^{15}\right)\bmod {10^9+7}$

解法

考虑哪些高斯整数 $i-1$ 表示第一位是 $1$

由于除以 $i-1$ 相当于逆时针旋转 $135^{\circ}$，模长再除以 $\sqrt{2}$

因此 $a+bi$ 的 $i-1$ 表示第一位 $\equiv a+b\pmod 2$

每次操作相当于对于一个整点，如果两维坐标和 $\equiv 1\pmod2$，那么将这个点左移一格，然后逆时针旋转 $135^{\circ}$。

我们考虑把整个正方形当成整体考虑，每个点记录当前时刻这个点对应多少个原来的点，以及这些点在已经计算过的位中 $1$ 的个数总和。

然后考虑对一个正方形连续做两次上述操作，留下来的点就是原先两维坐标都是 $2$ 的倍数的那些点。

这样操作后留下来的每个点 $\left(2p,2q\right)$ 的值都只依赖于操作前 $\left(2p-1,2q+1\right),\left(2p,2q+1\right),\left(2p,2q\right),\left(2p+1,2q\right)$ 这四个点对应的值。

然后，假设当前正方形的范围为 $\left[-L,L\right]$

若 $2\not\mid L$ ，那么在当前正方形外面补一圈全 $0$ 的点

然后做如上变换。

可以归纳证明，每次变换后正方形的值都至多只有 $25$ 个不同区域，即，上下左右 $2\times 2$ 的角，上下左右各两条棱，以及中间的正方形区域。

即形如下图的 $25$ 个区域

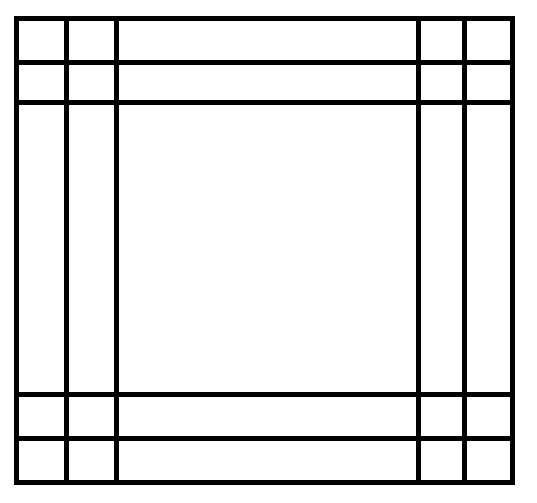
计算完变换后的值后还要顺时针旋转 $90^{\circ}$，对应两次操作分别逆时针旋转的 $135^{\circ}$

Project Euler 544 Chromatic Conundrum

题面

令 $F\left(r,c,n\right)$ 表示将 $r\times c$ 棋盘 $n$ 染色使得相邻格子不同色的方案数，旋转翻折相同的棋盘视为不同棋盘

求 $\displaystyle\sum_{i=1}^{1112131415}F\left(9,10,i\right)\pmod{10^9+7}$

解法

套路题，首先我们考虑轮廓线状压 dp

我们考虑使用最小表示法记录前 $r$ 个格子中哪些格子是相同的，那么状态数就是 $Bell\left(r\right)$

例如 $4$ 个格子的颜色为 $RBRGB$ ，那么它们的最小表示法 $12132$

设 $f\left(i,j\right)$ 表示当前处于位置 $i$，前面 $r$ 个格子的颜色的最小表示法是 $j$，假设 $j$ 用了 $k$ 种颜色，那么下一次转移如果新加入了一种颜色，系数就是 $n-k$，否则就是 $1$

由此我们可以发现 dp 数组关于 $n$ 是一个 $r\times c$ 次左右的多项式，我们分别求出 $n=1\sim r\times c$ 时的答案然后插值多项式即可

求答案时，我们用斯特林数把多项式化为下降幂形式 $\displaystyle \sum_{i=1}^kf_ix^{\underline{i}}$

然后使用 $\displaystyle \sum_{t=1}^nt^{\underline{i}}=i!\sum_{i=1}^n\binom{t}{i}=i!\binom{t+1}{i+1}=\dfrac{t^{\underline{i+1}}}{i+1}$ 计算答案即可

复杂度 $\mathcal{O}\left(r^3c^2Bell\left(r\right)\right)$

这题难度感觉没有 90% 啊

Project Euler 606 Gozinta Chains II

题面

对于正整数 $n$，定义正整数序列 $a_1,a_2\cdots a_m$ 是好的当前仅当 $a_1=1,a_m=n,\forall 1\lt i\le m,a_{i-1}\mid a_i,a_{i-1}\lt a_i$

求所有满足 $1\le n\le 10^{36}$ 且对于 $n$ 恰好存在 $252$ 个好的序列的 $n$ 的和 $\bmod 10^9$

解法

设 $n$ 的分解为 $\prod_{i=1}^k\alpha_i^{\beta_i}$

那么长度恰好为 $m$ 的序列个数为 $\displaystyle\sum_{i=0}^{m-2}\left(-1\right)^i\prod_{j=1}^k\binom{\beta_j+m-i-2}{m-i-2}$

令 $\prod_{j=1}^k\binom{\beta_j+x-1}{x-1}=\sum_{i\ge 1}f_i\binom{x}{i}$，套路，都是套路

$$ \begin{aligned} &\sum_{m\ge 1}\sum_{x=1}^{m}\left(-1\right)^{m-x}\binom{m}{x}\prod_{j=1}^{k}\binom{\beta_j+x-1}{x-1}\\ =&\sum_{m\ge 1}\sum_{x=1}^{m}\left(-1\right)^{m-x}\binom{m}{x}\sum_{i\ge 1}f_i\binom{x}{i}\\ =&\sum_{i\ge 1}f_i\sum_{m\ge 1}\sum_{x}\left(-1\right)^{m-x}\binom{m}{x}\binom{x}{i}\\ =&\sum_{i\ge1}f_i \end{aligned} $$

其实不用那么麻烦，直接搜索也是能搜出来的，形式为 $p^3q^3$

min_25 筛筛出 $1e12$ 范围内的所有前缀的 $p^3$ 之和最后再做一遍整除分块计算答案即可。

Project Euler 792 Too Many Twos

题面

定义 $S\left(n\right)=\sum\limits_{k=1}^n\left(-2\right)^k\binom{2k}{k}$，$u\left(n\right)=\nu_2\left(3S\left(n\right)+4\right)$，其中 $\nu_2\left(k\right)$ 表示最大的非负整数 $t$ 使得 $2^t\mid k$ 。

求 $\sum_{i=1}^{10^4}u\left(i^3\right)$

解法 & 社论

打表 $u\left(1\right)\sim u\left(1000\right)$，猜测 $u\left(n\right)=n+\mathcal{O}\left(\log n\right)$。

再打表 $\dfrac{\left|3S\left(n\right)+4\right|}{2^{n+2}}$，发现是OEIS A026641，然后看到有一条公式给出了下列式子

$$ a\left(n\right)=\sum_{k=0}^n\left(-2\right)^k\binom{2n+1}{k+n+1} $$

由于猜测 $u\left(n\right)-n$ 是 $\mathcal{O}\left(\log n\right)$ 的，因此 $k$ 很大的项对于答案是没有影响的，我们也只要考虑求出 $a\left(n\right)\bmod 2^{t}$，对于本题 $t=64$ 即可。

那么剩下的问题就变成了求 $\binom{2n+1}{k+n+1}\bmod 2^{64}$，由于 $2$ 在 $\bmod 2^{64}$ 意义下没有逆元，而且我们已知 $\nu_2\left(\binom{n+m}{n}\right)=\operatorname{popcount}\left(n\& m\right)$，因此我们只要求出 $\dfrac{k!}{2^{\nu_2\left(k!\right)}}$ 即可

注意到对于满足 $\forall 1\le i\le k,a_{i}\ge 2^{q}$ 的数列 $a_i$，而且注意到

$$ \prod_{i=1}^{k}a_i=\prod_{i=1}^k\left(a_i-2^q+2^q\right)=\sum_{j=0}^k\sum_{\left|S\right|=j,S\subseteq \left[k\right]}2^{q\left|S\right|}\prod_{i\not \in S}\left(a_i-2^q\right) $$

这个式子只有前 $\frac{64}{q}$ 项是有用的，所以我们考虑 dp

令 $f\left(i,j\right)$ 表示 $\displaystyle f\left(i,j\right)=\sum_{\left|S\right|=j,S\subseteq\left\{1,3,\dots,2^i-1\right\}} \prod_{i\in \left\{1,3,\dots 2^i-1\right\}\backslash S} i$，即 $2^i$ 范围内的奇数有 $j$ 个不选的方案的乘积之和。

那么有转移：$\displaystyle f\left(i,j\right)=\sum_{k}\sum_{t}\binom{j}{t}2^{\left(i-1\right)t}f\left(i-1,j-t\right)f\left(i-1,k\right)$

对于每个 $i$，$j$ 只需枚举到 $\min\left(2^{i-1},\sum_{j\ge i}\frac{64}{j-1}\right)$ 即可。

计算答案时，我们先算出 $1\sim k$ 中所有奇数的乘积。

按位将 $1\sim k$ 中的奇数划分成 $\mathcal{O}\left(\log k\right)$ 个区间，每个区间形如 $\left[m,m+2^i\right)$ 其中 $m$ 满足 $2^i\mid m$

那么对于每段区间位置按 $\left(a_t-m+m\right)$ 拆开用 $f\left(i\right)$ 计算即可

再将 $k$ 赋值为 $\left\lfloor\frac{k}{2}\right\rfloor$ 重复以上过程，此时可以算出原来恰包含 $1$ 个 $2$ 的项的积，不断重复直到 $k$ 变为 $0$ 即可。

代码耗时：30s

社论1：

求 $k!\bmod 2^{64}$

把它变成 $\bmod 2^{65}$，然后使用式子（其中 $\displaystyle \left(k\right)_p=\prod_{i=1,p\;\not \mid\;i}^{k}i$）

$$ \begin{aligned} \left(up!\right)_p\equiv& \pm \prod_{j=1}^{r}\left(jp!\right)_p^{\beta_j}\pmod {p^{2r+1}}\\ \left(\beta_j=\beta_{r,j}\left(i\right)\right):=&\dfrac{u}{j}\prod_{1\le i\le r,i\ne j}\left(\dfrac{u^2-i^2}{j^2-i^2}\right) \end{aligned} $$

正负性用两边 $\bmod 4$ 判断，式子出处

社论2：

OEIS式子证明：咕咕咕

社论3：

不用 OEIS 式子的做法：

$$ u\left(n+m\right)=\nu_2\left(3S\left(n+m\right)+4\right)=\nu_2\left(4+\sum_{i=1}^n\left(-2\right)^i\binom{2i}{i}+\sum_{k=n+1}^{n+m}\left(-2\right)^k\binom{2k}{k}\right) $$

对于足够大的 $m$，有 $\nu_2\left(n+m\right)\gt \nu_2\left(n\right)$

因此有 $\displaystyle\nu_2\left(\sum_{k=n+1}^{n+m}\left(-2\right)^k\binom{2k}{k}\right)=\nu_2\left(n\right)$。跟上面一样计算 $\mathcal{O}\left(\log n\right)$ 项即可。