线性代数相关

矩阵相关

矩阵的秩

矩阵的秩为线性无关的行/列的数量的最大值，其中行秩等于列秩

且 $\operatorname{rank}\left(A\times B\right)\le \min\left(\operatorname{rank}\left(A\right),\operatorname{rank}\left(B\right)\right)$

高斯消元

高斯消元通过初等行变换将 $n\times n$ 矩阵 $A$ 分解为 $PLU$ 形式，用来解决方程 $A\mathrm{x}=b$，其中 $P$ 为置换矩阵，$L$ 为下三角矩阵，$U$ 为上三角矩阵

高斯消元还可以扩展为求逆矩阵，将 $\left[\begin{matrix}A &I\end{matrix}\right]$ 高斯消元后即为 $\left[\begin{matrix}I &A^{-1}\end{matrix}\right]$，因为$\left[\begin{matrix}A &I\end{matrix}\right]\times A^{-1}=\left[\begin{matrix}I &A^{-1}\end{matrix}\right]$

高斯消元将 $\left[\begin{matrix}A&b\end{matrix}\right]$ 乘以 $L^{-1}P$ 得到 $\left[\begin{matrix}U&L^{-1}Pb\end{matrix}\right]$ 进行求解，因此，若一个线性方程组 $A\mathrm{x}=b$ 中 $A$确定，$b$ 不确定，可以 $\mathcal{O}\left(n^3\right)$ 预处理消元单次 $\mathcal{O}\left(n^2\right)$ 回答询问。

逆矩阵

对于 $n\times n$ 的矩阵 $A$，若存在 $n\times n$ 的矩阵 $B$ 使得 $AB=BA=I_n$，则称 $B$ 为 $A$ 的逆矩阵，且 $A$ 可逆当且仅当 $A$ 是满秩的。

矩阵乘法的逆：对于可逆方阵 $A,B$，$\left(AB\right)^{-1}=B^{-1}A^{-1}$
$A^{-1}$ 满足 $\det\left(A^{-1}\right)\det\left(A\right)=1$

特征值

对于 $n\times n$ 的方阵 $A$，若存在 $n$ 维非零列向量 $\mathrm{x}$ 使得 $A\mathrm{x}=\lambda\mathrm{x}$ ，那么称 $\lambda$ 为 $A$ 的特征值

特征多项式

对于 $n\times n$ 矩阵 $A$，定义它的特征多项式 $p_A\left(x\right)=\det\left(xI_n-A\right)$，这样这个多项式永远是首一的，且这个多项式的根为全体特征值。

对于复杂度不那么严格的应用场景，可以直接 $\mathcal{O}\left(n^4\right)$ 插值算出特征多项式

求上 Hessenberg 矩阵特征多项式

对于形如

$$ H=\left[\begin{matrix}\alpha_1 &h_{12}&\dots &\dots &h_{1n}\\\beta_2 &\alpha_2 &h_{23}&\dots &\vdots\\&\ddots &\ddots &\ddots &\vdots \\&&\ddots &\ddots &h_{\left(n-1\right)n}\\&&&\beta_{n}&\alpha_{n}\end{matrix}\right] $$

的上海森堡矩阵，令 $p_i\left(x\right)$ 为左上角 $i\times i$ 的子矩阵的特征多项式，那么 $\displaystyle p_i\left(x\right)=\left(x-\alpha_i\right)p_{i-1}\left(x\right)-\sum_{m=1}^{i-1}h_{i-m,i}\left(\prod_{j=i-m+1}^i\beta_j\right)p_{i-m-1}\left(x\right)$

时间复杂度 $T\left(n\right)=T\left(n-1\right)+\mathcal{O}\left(n^2\right)=\mathcal{O}\left(n^3\right)$

按照最后一行余子式展开，
$$ p_n\left(x\right)=\left(x-\alpha_n\right)p_{n-1}\left(x\right)+\beta_n\cdot \det\left(\left[\begin{matrix}x-\alpha_1 &\dots &-h_{1,n-2} & -h_{1,n}\\-\beta_2 &\ddots &\ddots &\vdots \\&\ddots& x-\alpha_{n-2}&-h_{n-2,n}\\&&-\beta_{n-1}&-h_{n-1,n}\end{matrix}\right]\right) $$
不断展开即可，每一项即为一个后缀的 $\beta_{j},k\lt j\le n$ 和 $-h_{k}$，于是就可以得到上述式子，其中，边界条件为 $p_0\left(x\right)=1$

求一般矩阵的特征多项式

对于和 $A$ 相似的矩阵 $P^{-1}AP$，$\det\left(xI_n-P^{-1}AP\right)=\det\left(P^{-1}xI_nP-P^{-1}AP\right)=\det\left(xI_n-A\right)\cdot \det\left(P^{-1}\right)\cdot \det\left(P\right)=p_A\left(x\right)$

所以考虑对 $A$ 做相似变换使得特征多项式好求，

由于高斯消元对应的行变换矩阵（第 $j$ 行加上第 $i$ 行的 $k$ 倍）为 $\displaystyle \left(T_{i,j}\left(k\right)\right)_{u,v}=\begin{cases}1 &u=v\\k &u=i,v=j\\0 & \text{others}\end{cases}$，对应的逆矩阵为 $\displaystyle \left(T_{i,j}\left(k\right)\right)^{-1}_{u,v}=\begin{cases}1 &u=v\\-k &u=i,v=j\\0 & \text{others}\end{cases}$，因此对 $A$ 做 $TAT^{-1}$ 变换相当于第 $j$ 行加上第 $i$ 行的 $k$ 倍以后第 $i$ 列加上第 $j$ 列的 $-k$ 倍。

当我们对主对角线进行消元时，这样的操作会使已经消好的列变得非零。而如果对此对角线进行消元，假设消到第 $i$ 列，每次操作对应的是第 $i+1$ 行和第 $j\left(j\gt i+1\right)$ 行，那么不会影响到第 $i$ 列。因此，可以将任意矩阵通过相似变换变成上海森堡矩阵然后求特征多项式。

具体而言，我们每次选择 $A_{i+1,i}$ 作为主元，如果此时 $A_{i+1,i}$ 为 $0$ 则找到一个 $j\ge i+1$ 使得 $A_{j+1,i}$ 非零，然后做 $i:=i+j$ 初等行变换，如果找不到直接跳过这一个主元，接下来对 $j=i+2\sim n$ 依次用第 $i$ 行消去第 $j$ 行。每次做行变换时，假设是第 $i$ 行加上 $k$ 倍的第 $j$ 行，那么做完后还要做一遍，第 $j$ 列加上 $-k$ 倍的第 $i$ 列。

Code:

void calc(int n){
    static int dat[N][N];dat[0][0]=1;
    for(int i=1;i<n;++i){
        int pos=0;
        for(int j=i+1;j<=n;++j) if(mat[j][i]){pos=j;break;}
        if(!pos) continue;
        if(pos!=i+1){
            for(int j=i;j<=n;++j) redu(mat[i+1][j],mat[pos][j]);
            for(int j=1;j<=n;++j) redu(mat[j][pos],p-mat[j][i+1]);
        }
        int iv=fp(mat[i+1][i],p-2);
        for(int j=i+2;j<=n;++j){
            int num=1ull*iv*mat[j][i]%p;
            for(int k=i;k<=n;++k) redu(mat[j][k],p-1ull*num*mat[i+1][k]%p);
            for(int k=1;k<=n;++k) redu(mat[k][i+1],1ull*num*mat[k][j]%p);
        }
    }
    for(int i=1;i<=n;++i){
        dat[i][0]=redu(p-1ull*dat[i-1][0]*mat[i][i]%p);dat[i][i]=dat[i-1][i-1];
        for(int j=1,t=mat[i][i];j<i;++j) dat[i][j]=redu(dat[i-1][j-1]+p-1ull*t*dat[i-1][j]%p);
        for(int j=i-1,t=mat[i][i-1];j;--j,t=1ull*t*mat[j+1][j]%p) for(int k=0;k<j;++k) redu(dat[i][k],p-1ull*dat[j-1][k]*t%p*mat[j][i]%p);
    }
    for(int i=0;i<=n;++i) ans[i]=dat[n][i];
}

应用

可以在已知特征多项式的情况下在 $\mathcal{O}\left(n\log^2n\right)$ 的时间内求常系数齐次线性递推。

行列式相关

矩阵树定理

对于一张无自环有向图令 $e\left(u,v\right)$ 表示 $u\rightarrow v$ 的所有边的边权和，定义矩阵 $L^{in}\left(G\right),L^{out}\left(G\right)$ 为：

$$ \begin{aligned} L^{in}\left(G\right)_{u,v=1}^n&=\begin{cases}\displaystyle\sum_{k=1}^ne\left(k,u\right) &u=v\\-e\left(u,v\right) &u\neq v\end{cases}\\ L^{out}\left(G\right)_{u,v=1}^n&=\begin{cases}\displaystyle\sum_{k=1}^ne\left(u,k\right) &u=v\\-e\left(u,v\right) &u\neq v\end{cases} \end{aligned} $$

那么 $L^{in}$ 去掉第 $i$ 行第 $i$ 列后的行列式即为以 $i$ 为根的所有外向树的边权乘积之和，$L^{out}$ 去掉第 $i$ 行第 $i$ 列后的行列式即为以 $i$ 为根的所有内向树的边权乘积之和。

一些相关结论：

完全二分图的生成树个数：$n^{m-1}m^{n-1}$
BEST定理：对于有向欧拉图 $G$，$G$ 的不同欧拉回路个数即为 $\displaystyle \prod_{v\in V}\left(\operatorname{deg}\left(v\right)-1\right)!\times$ 以任意点 $u$ 为根的内向生成树个数。
由此可以得出，有向欧拉图的所有点的内向生成树个数是一样多的。
生成树相关，钦定每个点的度数为 $d_i$ 的完全图的生成树个数为 $\dfrac{\left(n-2\right)!}{\prod\left(d_i-1\right)!}$，因为每个点恰好在 prufer 序列中出现了 $d_i-1$ 次。

LGV引理

设 $G$ 为一个有向无环图，$w\left(e\right)$ 表示 $e$ 的边权，$W\left(P\right)$ 表示 $P$ 这条路径的 $w\left(e\right)$ 的乘积，$e\left(u,v\right)=\displaystyle\sum_{P:u\rightarrow v}W\left(P\right)$ ，即 $u\rightarrow v$ 的每条路径的边权乘积之和。

定义一组 $A_1,A_2\cdots A_n$ 到 $B_1,B_2\dots B_n$ 的路径集合 $S_1,S_2\cdots S_n$ 为不交路径，当前仅当存在 $n$ 阶置换 $\sigma$ 使得 $S_i$ 为 $A_i$ 到 $B_{\sigma\left(i\right)}$ 的路径，且 $\forall1\le i\lt j\le n$ $S_i,S_j$ 无公共顶点，令 $\operatorname{sign}\left(\sigma\right)$ 表示 $-1$ 的 $\sigma$ 逆序对数次方。

那么

$$ \det\left(e\left(A_i,B_j\right)\right)_{i,j=1}^n=\sum_{S_1,S_2,\dots,S_n:A\rightarrow B} \operatorname{sign}\left(\sigma\left(S\right)\right)\prod_{i=1}^nW\left(P\right) $$

即统计 $A\rightarrow B$ 中每对不相交路径的带权和，权为对应点匹配的符号。

Cauchy-Binet 定理

假设 $A$ 是 $m\times n$ 的矩阵，$B$ 是 $n\times m$ 的矩阵

$$ \det\left(A\times B\right) =\sum_{S\subseteq\binom{\left|n\right|}{m}}\det\left(A_{1\dots m,S}\right)\cdot \det\left(B_{S,1\dots m}\right) $$

例：愚蠢的在线法官
给定树和 $A_1,A_2\cdots A_k$ 求
$$ \begin{aligned} \det\left(\left[\begin{matrix}\operatorname{LCA}\left(A_1,A_1\right)&\operatorname{LCA}\left(A_1,A_2\right)&\cdots&\operatorname{LCA}\left(A_1,A_k\right)\\\operatorname{LCA}\left(A_2,A_1\right)&\ddots&&\operatorname{LCA}\left(A_2,A_k\right)\\\vdots&&\ddots&\vdots\\\operatorname{LCA}\left(A_k,A_1\right)&\operatorname{LCA}\left(A_k,A_2\right)&\cdots&\operatorname{LCA}\left(A_k,A_k\right) \end{matrix}\right] \right)\pmod {998244353},\; n,k\le 5\times 10^5 \end{aligned} $$

首先联想到 $\gcd$ 矩阵的求法

$$ \det\left(\gcd\left(i,j\right)\right)_{i,j=1}^n=\det\left(\left[j\mid i\right]\right)_{i,j=1}^n\cdot \det\left(\left[i\mid j\right]\phi\left(i\right)\right)_{i,j=1}^n=\prod_{i=1}^n\phi\left(i\right) $$

因此先对 $v$ 做树上差分，$v_{u}^{\prime}=v_{u}-v_{fa_u}$，再构造矩阵 $B_{k\times n},C_{n\times k}$ ，定义 $i\rightarrow j$ 表示 $i$ 是 $j$ 的祖先，那么 $B_{i,j}=\left[j\rightarrow i\right]v_{j}^{\prime}$ ，$C_{i,j}=\left[i\rightarrow j\right]$

那么 $\displaystyle\det\left(B\times C\right) =\sum_{S\subseteq\binom{\left|n\right|}{k}}\det\left(B_{1\dots k,S}\right)\cdot \det\left(C_{S,1\dots k}\right)$

考虑上面这个式子对应的组合意义，从 $\left[n\right]$ 中选出 $k$ 个点组成集合 $S$，然后对 $A_i$ 到 $S_i$ 的路径数是 $v_{S_i}^{\prime}\cdot \left[S_i\rightarrow A_i\right]$，的不交路径数求和，由于任意不同 $S$ 对应的路径集合无交，因此不会重复计数。

原问题转化为对 $A_1,A_2,\cdots A_k$ 找一个匹配点使得两两路径无交，匹配权是 $\prod_{v\in S}v_i^{\prime}$，树形 $dp$ 即可。

线性基

求法

从第 $1$ 位开始一次消去每一位，直到不能消去位置，那么这一位是一个新的主元，加入线性基即可。

区间线性基

考虑扫描线，维护 $r=k$ 时的答案。

考虑改变加入的方式使得对于每一时刻，假设线性基第 $i$ 位的主元加入时刻为 $t_i$，那么 $t_i$ 依次递减，这样询问时只需考虑一个前缀的主元即可。

考虑每次消元时如果当前主元加入时间早于当前被消对象，那么交换两者，继续消元，这样每次线性基主元加入时间就是递减的了。

数论相关

基本定理

欧拉定理与扩展欧拉定理：$a^{c}\equiv\begin{cases}a^{c\;\bmod{ \;\phi\left(m\right)}} &\gcd\left(a,m\right)=1\\a^{c} &\gcd\left(a,m\right)\ne 1 \;\land\; c\lt \phi\left(m\right)\\a^{c\;\bmod{ \;\phi\left(m\right)}+\phi\left(m\right)} &\gcd\left(a,m\right)\ne 1 \;\land \; c\ge \phi\left(m\right)\end{cases}$

莫比乌斯反演：$\sum\limits_{i\mid n}\mu\left(i\right)=\left[n=1\right]$

原根与阶：对于任意 $a,m$，若 $\gcd\left(a,m\right)=1$，那么 $\operatorname{ord}_m\left(a\right)\mid \phi\left(m\right)$

因此，求原根只需对 $\phi\left(p\right)$ 的每个质因子 $k$ 判断 $a^{\frac{\phi\left(p\right)}{k}}\equiv 1\pmod p$ 是否满足即可

有原根的数：$2,4,p^k,2p^k$

数论分块

令 $S\left(n\right)=\left\{\left\lfloor\dfrac{n}{i}\right\rfloor\mid 1\le i\le n\right\}$，那么 $\left|S\left(n\right)\right|=\mathcal{O}\left(\sqrt{n}\right)$，且 $\forall i\in S\left(n\right),S\left(i\right) \subseteq S\left(n\right)$，因为 $\left\lfloor\dfrac{n}{ij}\right\rfloor=\left\lfloor\dfrac{\left\lfloor\frac{n}{i}\right\rfloor}{j}\right\rfloor$，这也是筛法的基础条件。

筛法

Powerful Number 筛

对于 $n=\prod p_i^{\alpha_i}$ ，若 $\forall i,\alpha_i\ge 2$，那么称 $n$ 为 Powerful Number，

由于所有 Powerful Number 的都可以表示为 $a^2b^3,a,b\in \mathbb{N}$，所以 $n$ 以内的 Powerful Number 的个数为 $\displaystyle \int_1^{\sqrt{n}}\sqrt[3]{\frac{n}{x^2}}dx=\mathcal{O}\left(\sqrt{n}\right)$。

假设我们要求的积性函数为 $f\left(n\right)$ ，那么我们需要找到一个快速求前缀和的积性函数 $g\left(n\right)$，满足 $\forall p\in \mathbb{P},g\left(p\right)=f\left(p\right)$

假设 $g\left(n\right)\circ h\left(n\right)=f\left(n\right)$，那么 $f\left(p\right)=g\left(1\right)h\left(p\right)+g\left(p\right)h\left(1\right)=f\left(p\right)+h\left(p\right)$

那么 $h\left(p\right)=0$，于是 $h$ 只在 Powerful Number 处有值。

由于 $\displaystyle \sum_{i=1}^nf\left(i\right)=\sum_{i=1}^n\sum_{j\mid i}h\left(j\right)g\left(\frac{i}{j}\right)=\sum_{i=1}^nh\left(i\right)\sum_{j=1}^{\left\lfloor \frac{n}{i}\right\rfloor }g\left(j\right)$

而 $h\left(i\right)$ 只在 $\mathcal{O}\left(\sqrt{n}\right)$ 个数处有非零值，于是我们只需 dfs 枚举 Powerful Number 即可

复杂度

所有 Powerful Number 的 $-s$ 次方的和为

$$ \begin{aligned} \prod_{p}\left(1+\dfrac{1}{p^s\left(p^s-1\right)}\right)=&\prod_{p}\left(\dfrac{\left(p^{2s}-p^s+1\right)\left(p^{2s}+p^s+1\right)\left(p^{2s}-p^s\right)}{p^s\left(p^s-1\right)\left(p^{2s}+p^s+1\right)\left(p^{2s}-p^s+1\right)}\right)\\=&\prod_{p}\left(\dfrac{p^{6s}-p^{4s}-p^{3s}+1}{p^{6s}-1}\right)\\ =&\prod_p\left(\dfrac{1-p^{-6s}}{\left(1-p^{-2s}\right)\left(1-p^{-3s}\right)}\right)\\ =&\dfrac{\zeta\left(2s\right)\zeta\left(3s\right)}{\zeta\left(6s\right)} \end{aligned} $$

因此，对于能单点 $\mathcal{O}\left(n^{\alpha}\right)$ 求前缀和的 $g\left(n\right)$，总复杂度为 $\displaystyle \mathcal{O}\left(\max\left(\sqrt{n},n^{\alpha}\cdot \frac{\zeta\left(2\alpha\right)\zeta\left(3\alpha\right)}{\zeta\left(6\alpha\right)}\right)\right)$

例

$f\left(p^k\right)=p$，令 $g\left(n\right)=n$，复杂度 $\mathcal{O}\left(\sqrt{n}\right)$
$f\left(p^k\right)=k+1$，令 $g\left(n\right)=\sigma_0\left(n\right)$，复杂度 $\mathcal{O}\left(\sqrt{n}\log n\right)$
$f\left(p^k\right)=p\otimes c$，对于 $p\neq 2$，$p\otimes 1=p-1$，令 $g\left(n\right)=\varphi\left(n\right)$，容斥一下 $2$ 的次幂即可，复杂度 $\mathcal{O}\left(n^{\frac{2}{3}}\right)$

min_25 筛

min_25 筛支持质数和质数的幂处比较好求的积性函数，例如 LOJ#6053. 简单的函数

积性函数的形式可以不只是一个数，也可以是满足交换律的对象。

例：质数计数2
求 $1\sim n$ 中 $\bmod m$ 为 $0,1,\dots m-1$ 的质数个数，$1\le n\le 3\times 10^{10},3\le m\le 11,m$ 为质数

在 min_25 筛前缀质数个数时，我们对于每个前缀维护当前 $\bmod m$ 为 $0,1,\cdots m-1$ 的个数

在进行 $S\left(n\right) -S\left(t\right)\times p$ 操作时，

假设 $t$ 对应的前缀个数为 $b_0,b_1,\cdots b_{m-1}$，$p$ 在 $\bmod m$ 意义下的逆元是 $p^{-1}$

那么 $p,2p,\cdots pt$ 对应的前缀个数就是 $b_{0\times p^{-1}\pmod m},b_{1\times p^{-1}\pmod m},\cdots b_{\left(m-1\right)\times p^{-1}\pmod m}$

筛即可，比普通的筛复杂度多一个 $m$

杜教筛

杜教筛求函数 $f$ 前缀和需要找到函数 $g$ 使得 $f,g$ 的狄利克雷卷积 $h=f\cdot g$ 和 $g$ 的前缀和均可以快速计算

然后使用 $\displaystyle\sum_{i=1}^nh\left(i\right)=\sum_{i=1}^n\sum_{j=1}^n\left[ij\le n\right]f\left(i\right)g\left(j\right)$ 推出 $\displaystyle Sum_f\left(n\right)=\frac{1}{g\left(1\right)}\left(Sum_h\left(n\right)-\sum_{j\ge 2}g\left(j\right)Sum_f\left(\left\lfloor\dfrac{n}{j}\right\rfloor\right)\right)$ 计算

预处理 $k\le n^{\frac{2}{3}}$ 时的 $Sum_f\left(k\right)$ 使得复杂度达到 $\mathcal{O}\left(n^{\frac{2}{3}}\right)$

例：Project Euler 415 Titantic Sets
设一个整点点集是“好的”当且仅当存在一条直线经过恰好两个点，求所有点的两维坐标均在 $\left[0,N\right]$ 内的“好的”的点集个数 $n\le 10^{11}$

我们考虑不合法的点集是什么样的。

考虑证明对于任意一个不全共线的点集 $S$ ，必存在一条直线恰好经过 $S$ 中的两个点

proof

如果不存在，即任意经过两个点的直线经过第三个点。

设 $T$ 为所有经过 $S$ 中的两个点的直线组成的集合

$G=\left\{\left(u,l\right)\mid \operatorname{dist}\left(u,l\right)\neq 0,u\in S,l \in T\right\}$ ，由于所有点不全共线，因此 $G$ 不为空，且 $G$ 有限

因此我们取 $G$ 中 $\operatorname{dist}\left(u,l\right)$ 最小的元素，假设为 $\left(u_0,l_0\right)$

由于 $l_0$ 经过 $S$ 中的两个点，因此 $l_0$ 至少经过 $S$ 中的三个点，假设为 $A,B,C$

作 $u_0D\perp l_0$ ，垂足为 $D$

根据抽屉原理， $A,B,C$ 至少有两个在 $D$ 同侧（包含 $D$ ），假设为 $A,B$ ，且 $B$ 在线段 $AD$ 上

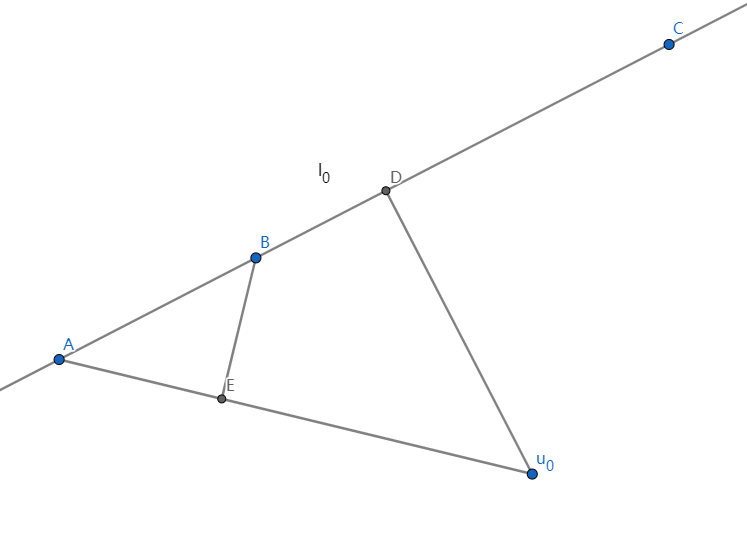
作 $BE\perp Au_0$，垂足为 $E$

由于 $\angle ABu_0\ge \angle ADu_0=90^{\circ}>\angle Au_0D\ge \angle Au_0B$

所以 $Au_0> AB$，$BE=\dfrac{2S_{\triangle ABu_0}}{Au_0}<\dfrac{2S_{\triangle ABu_0}}{AB}=Du_0$

因此 $\left(B,Au_0\right)$ 比 $\left(u_0,l\right)$ 更优，矛盾！

所以任意不合法的点集所有点必共线，然后就可以愉快的推式子了。以下只考虑 $\ge3$ 个点的情况

我们对于竖直，水平，斜 $45^{\circ}$ 和其他直线分别计算

对于最后一种

$$ \begin{aligned} Ans=4\sum_{i\ge 2}\sum_{1\le k\le i} \left[\gcd\left(i,k\right)=1\right]\sum_{j=1}^{\left \lfloor \frac{N}{j}\right \rfloor}\left(N+1-i\cdot j\right)\left( N+1-k\cdot j\right) \cdot \left(2^{j-1}-1\right) \end{aligned} $$

化简完是关于 $\phi\left(i\right),i\phi\left(i\right),i^2\phi\left(i\right)$ 的形式

设 $g_k\left(i\right)=i^k$

那么 $\left(\left(i^k\phi\left(i\right)\right)\circ g_k\right)\left(j\right)=j^{k+1}$，于是就可以愉快的用杜教筛了，时间复杂度 $\mathcal{O}\left(n^{\frac{2}{3}}\right)$

二次剩余与高斯整数

对于奇质数 $p$ 和 $n,p\not \mid n$，若存在 $x\in \mathbb{Z},x^2\equiv n\pmod p$ ，则称 $n$ 为 $\bmod p$ 的二次剩余

定义勒让德符号 $\left(\dfrac{n}{p}\right)=\begin{cases}1 &n\;是\bmod p\;的二次剩余\\-1 &n\;不是\bmod p\;的二次剩余\\0 &n=0\end{cases}$

则有 $\displaystyle\left(\dfrac{n}{p}\right)\equiv n^{\frac{p-1}{2}}\pmod p$

证明：$p$ 为奇质数因此 $p$ 有原根 $g$，令 $n\equiv g^k\pmod p$ ，则 $g$ 为偶数时，$n$ 为二次剩余，此时 $\displaystyle n^{\frac{p-1}{2}}\equiv g^{p-1}\equiv 1\pmod p$

$g$ 为奇数时，$n$ 不是二次剩余，此时 $\displaystyle n^{\frac{p-1}{2}}\equiv g^{\frac{p-1}{2}}\equiv -1\pmod p$ ，因为 $p-1$ 是使得 $g^k\equiv 1\pmod p$ 的最小正整数 $k$ ，且 $1$ 只有 $\pm1$ 两个平方根

由此还可以得出一个结论，勒让德符号是完全积性的

高斯二次互反律：

$$ \left(\dfrac{p}{q}\right)\cdot\left(\dfrac{p}{q}\right)=\left(-1\right)^{\frac{p-1}{2}\cdot \frac{q-1}{2}} $$

求 $n$ 的二次剩余：
随机 $a$ 直到 $w=a^2-n$ 不是二次剩余，则 $\left(a+\sqrt{w}\right)^{\frac{p-1}{2}}$ 为一个解，在 $\mathbb{Z}_p\left[\sqrt{w}\right]$ 上快速幂即可

高斯整数：$\mathbb{Z}\left[i\right]=\left\{a+bi\mid a,b\in \mathbb{Z}\right\}$

定义平方分解数为可以表示为 $a^2+b^2,a,b\in \mathbb{Z}$ 的正整数

平方分解数的积是平方分解数
平方分解数被素平方分解数整除的商是平方分解数
平方分解数被非平方分解数整除的商必有非平方分解因子
若 $\left(a,b\right)=1$，则 $a^2+b^2$ 的所有因子都是平方分解数
$4n+1$ 素数都是平方分解数

定义高斯整数的除法：

令 $\frac{a}{b}=x+yi$，那么 $\left\lfloor\frac{a}{b}\right\rfloor=\left\lfloor x+\frac{1}{2}\right\rfloor+\left\lfloor y+\frac{1}{2}\right\rfloor i$，根据除法再定义 $\gcd$

求 $4n+1$ 型素数的高斯整数分解
随机出一个非二次剩余 $t$，令 $k=t^n$，令 $u=\gcd\left(p,k+i\right)$ ，则 $p=u\overline{u}$
求 $x^2+y^2=n$ 的所有正整数解
即将 $n$ 分解为共轭高斯整数的积，先将 $n$ 质因数分解，此时 $4k+3$ 型素数次数必须为偶数，在 $u,\overline{u}$ 中均分，对于 $2$，将 $\left(1+i\right)$ 分给 $u$，其余给 $\overline{u}$，对于 $4k+1$ 型素数，$v^t\overline{v}^t$ 分给 $u$ $v^i\overline{v}^{t-i}$ 即可。

不定方程

一些常用的不定方程

$x^2+y^2=z^2$ 的所有 $\gcd\left(x,y,z\right)=1$ 的解满足 $x=m^2-n^2,y=2mn,z=m^2+n^2,\left(\left(m,n\right)=1,m\not\equiv n\pmod 2\right)$

$x^2+py^2=z^2$ ( $p$ 是素数) 的所有 $\gcd\left(x,y,z\right)=1$ 的解满足 $x=\dfrac{\left(m^2-pn^2\right)}{2},y=mn,z=\dfrac{m^2+pn^2}{2}\left(m\gt n\sqrt{p}\right)$

Pell 方程：对于方程 $x^2-dy^2=1\left(d\in \mathbb{N},\sqrt{d}\not\in \mathbb{N}\right)$，令 $x_0,y_0$ 为满足方程的 $x+y\sqrt{d}$ 最小的一组解，那么方程的所有解 $x_i,y_i$ 均满足 $\exists\;t\in \mathbb{N},x_i+y_i\sqrt{d}=\left(x_0+y_0\sqrt{d}\right)^t$

多元一次不定方程

求 $\displaystyle \sum_{i=1}^n k_ix_i=m\left(\forall i,k_i\ge 1\right)$ 的非负整数解组数。

令 $T=\operatorname{lcm}\left(k_i\right),p_i=x_i\bmod \frac{T}{k_i},r_i=\left\lfloor\dfrac{x}{\frac{T}{k_i}}\right\rfloor$，那么合法的 $p_i,r_i$ 和非负整数解之间构成双射，确定 $\sum p_i\cdot k_i=l$ 后剩下的 $r$ 的方案数可以直接由 $\displaystyle \binom{\frac{m-r}{T}+n-1}{n-1}$ 得到，因此背包算出 $l$ 对应的方案数即可，复杂度 $\mathcal{O}\left(\operatorname{lcm}\left(k_i\right)\cdot n^2\right)$

概率与期望

概率分布函数和概率密度函数

这段可能在胡扯

对于一个连续随机变量 $X$，假设它的概率函数为 $P\left(k\right)=\Pr\left(X=k\right)$

那么它的概率分布函数 $\displaystyle F\left(k\right)=\Pr\left(X\le k\right)=\int_{-\infty}^kP\left(t\right)dt$

概率密度函数为 $\displaystyle f\left(k\right)=\lim_{\Delta\rightarrow 0}\dfrac{F\left(k+\Delta\right)-F\left(k\right)}{\Delta}$

那么 $X$ 的期望即为 $$\displaystyle \int_{-\infty}^{\infty}t\cdot \Pr\left(X=t\right)dt=\int_{-\infty}^{\infty}\Pr\left(X=t\right)\cdot\left(\int_{0}^{t}1dx\right)dt=\int_{0}^{\infty}\int_{x}^{\infty}\Pr\left(X=t\right)dtdx-\int_{-\infty}^0\int_{-\infty}^{x}\Pr\left(X=t\right)dtdx=\int_0^{\infty}\left(1-F\left(x\right)\right)dx-\int_{-\infty}^0F\left(x\right)dx$$

例：地震后的幻想乡
给定 $n$ 个点 $m$ 条边的无向连通图，每条边在 $\left[0,1\right]$ 中均匀随机，求生成树最大边最小值的期望。$n\le 10,m\le \frac{n\left(n-1\right)}{2}$

即求最小生成树最大边的期望。

设 $F_S\left(k\right)\left(1\in S\right)$ 为 $S$ 中最大边 $\gt k$ 的概率，那么最大边最小值的期望就是 $\displaystyle \int_{0}^1F_{\left[n\right]}\left(t\right)dt$

令 $G\left(S,k\right)=\displaystyle \int_{0}^1F_S\left(t\right)\left(1-t\right)^kdt$

那么考虑枚举 $S$ 中 $\le k$ 的边组成的集合中包含 $1$ 的连通块，令 $e\left(U,V\right)$ 表示 $U,V$ 两个点集中间的边数

$$ \begin{aligned} G\left(S,k\right)&=\int_{0}^1F_S\left(t\right)\left(1-t\right)^kdt\\ &=\sum_{S_0\subset S,1\in S_0}\int_{0}^1F_{S_0}\left(t\right)\left(1-t\right)^{e\left(S_0,S\backslash S_0\right)+k}dt\\ &=\sum_{S_0\subset S,1\in S_0}\left(\dfrac{1}{1+k+e\left(S_0,S\backslash S_0\right)}\cdot G\left(S_0,k+e\left(S_0,S\backslash S_0\right)\right)\right) \end{aligned} $$

递推即可，其中 $k$ 只需枚举到 $m$ ，复杂度 $\mathcal{O}\left(3^nm\right)$

摘自 command_block 博客：
$\displaystyle 概率=\dfrac{方案数}{总方案数}$
$\displaystyle 期望 =\sum概率\cdot 对应权$
当一个很难求时考虑转化成其他来求。

例：PKUWC2018 猎人杀
给定 $n$ 和长为 $n$ 的序列 $w_i$，有 $n$ 个猎人，每次按 $w_i$ 带权随机干掉一个猎人，求 $1$ 最后被干掉的概率

首先有结论：如果每次可以杀死的猎人是全集，不断杀直到杀死一个未死的猎人，最后的概率不变
那么我们考虑 $1\sim n$全部死亡的期望步数 $f_1$ 和 $2\sim n$ 全部死亡的期望步数 $f_2$
那么 $1 $ 在 $2\sim n$ 之后死的情况就是 $1\sim n$ 全部死亡的步数大于 $2\sim n$ 全部死亡的步数的情况，这时两者的差的期望就是不断挑一个猎人杀死直到1死亡的期望步数，即 $\dfrac{1}{p_1}$
那么 $1$ 最后死的概率就是 $\dfrac{f_1-f_2}{\frac{1}{p_1}}$
考虑 $\min-\max$ 容斥求出 $f_1,f_2$

$$ f_1=\sum_{T\subseteq \left[n\right],T\neq \emptyset}\left(-1\right)^{\left|T\right|-1}\dfrac{1}{\sum_{i\in T}p_i} $$

由于 $\sum_{i\in T}p_i$ 只有可能是 $\dfrac{1}{\sum w_i},\dfrac{2}{\sum w_i}\dots \dfrac{\sum w_i}{\sum w_i}$，分治NTT背包算出所有的项即可

停时定理

鞅是一种离散时间的随机过程 $X_0,X_1,X_2,\dots$ 满足：

$E\left(\left|X_t\right|\right)<\infty$，$\forall t\ge 0$
$E\left(X_{t+1}-X_t\mid X_0,\dots X_t\right)=0，\forall t\ge 0,\forall X_0,\dots X_t$

设 $\tau$ 是 $X$ 的停止时间，使得 $\tau$ 只依赖于之前的过程而不是未来的过程

当 $\tau$ 满足一下三个条件之一时 $E\left(X_{\tau}\right)=X_0$

$\tau $ 几乎有界 (almost surely bounded) ，即存在一个常数 $c\in \mathbb{N}$ 使得 $\tau \le c$ 的概率为 $1$
$\tau$ 期望有限，$\left|X_{t+1}-X_t\right|$ 几乎有界，即 $E\left(\tau\right)\lt \infty$ 且存在一个常数 $c$ 使得对于 $t\lt \tau$ 的每个事件， $E\left(X_{t+1}-X_t\right)\le c$ 成立的概率为 $1$
$X_t$ 一致有界，即存在常数 $c$ 满足对于任意 $t\le \tau$，$\left|X_{t}\right|\le c$

一般 oi 中的应用符合第二个条件，定义势能函数 $\phi$ 使得 $X_t=\phi\left(t\right)+t$，且 $\phi\left(\tau\right)$ 为常数

那么 $E\left(\phi\left(\tau\right)\right)+E\left(\tau\right)=E\left(X_{\tau}\right)=X_0$，于是 $E\left(\tau\right)=X_0-\phi\left(\tau\right)$

例：Slime and Biscuits
有 $n$ 个人，每个人一开始有 $a_n$ 块饼干，每次随机从所有饼干中选一块给其余 $n-1$ 个人中的任何一个，求期望多少次可以使得一个人拥有所有的饼干 $n\le 10^5,\sum a_i\le 3\times 10^5$

构造函数 $f:\mathbb{N}\rightarrow \mathbb{Z}$，$\phi=\sum_{i=1}^nf\left(a_i\right)$

那么 $E\left(\phi\left(t+1\right)-\phi\left(t\right)\right)=-1$

令 $m=\sum{a_i}$

$$ \begin{aligned} E\left(\phi\left(t+1\right)-\phi\left(t\right)\right)&=\sum_{i=1}^{n}\dfrac{a_i}{m}\left(\sum_{j\ne i}\dfrac{1}{n-1}\left(f\left(a_j+1\right)-f\left(a_j\right)\right)+f\left(a_i-1\right)-f\left(a_i\right)\right) \\ &=\sum_{i=1}^n\dfrac{1}{n-1}\cdot \dfrac{m-a_i}{m}\cdot f\left(a_i+1\right)-\left(\dfrac{a_i}{m}+\dfrac{1}{n-1}\cdot \dfrac{m-a_i}{m}\right)\cdot f\left(a_i\right)+\dfrac{a_i}{m}\cdot f\left(a_i-1\right) \\ &=-1 \end{aligned} $$

那么

$$ \begin{aligned} 0=\dfrac{1}{n-1}\cdot \dfrac{m-k}{m}\cdot f\left(k+1\right)-\left(\dfrac{k}{m}+\dfrac{1}{n-1}\cdot \dfrac{m-k}{m}\right)\cdot f\left(k\right)+\dfrac{k}{m}\cdot f\left(k-1\right)+\dfrac{1}{n} \end{aligned} $$

有递推式

$$ f\left(k+1\right)=\dfrac{nm-m+\left(n^2-n\right)k\cdot f\left(k-1\right)-\left(n^2k+nm-2nk\right)f\left(k\right)}{nm-nk} $$

$f\left(0\right),f\left(1\right)$ 任意设均可

其他

万能欧几里得

例：类欧几里得
给定 $n,a,b,c$，分别求 $\displaystyle\sum_{i=0}^{n}\left\lfloor\dfrac{ai+b}{c}\right\rfloor,\sum_{i=0}^{n}\left\lfloor\dfrac{ai+b}{c}\right\rfloor^2,\sum_{i=0}^{n}i\left\lfloor\dfrac{ai+b}{c}\right\rfloor \pmod {998244353}$
$0\le n,a,b,c\le 10^9$

对于此类问题，一般定义两种符号 $U,R$ 分别表示遇到遇到一条 $y=k,k\in \mathbb{Z}$ 的直线和遇到一条 $x=k,x\in \mathbb{Z}$ 的直线，这样 $\left\lfloor\dfrac{ai+b}{c}\right\rfloor$ 的图像可以描述为 $y=\dfrac{ax+b}{c}$ 的一条直线产生的符号序列。一般而言 $U,R$ 为半群。

考虑递归解决这个问题，假设当前问题是 $\sum\limits_{i=0}^n\left\lfloor\dfrac{ai+b}{c}\right\rfloor\left(0\le b\lt c\right)$ ，当前的遇到横线的操作是 $U$，当前遇到竖线的操作是 $R$，其中 $U,R$ 可能由一个序列的原始 $U,R$ 构成。

如果 $a\ge c$ ，那么每次 $R$ 符号前一定对应了 $\left\lfloor\frac{a}{c}\right\rfloor$ 个 $U$，因此可以直接将 $R:=U^{\left\lfloor\frac{a}{c}\right\rfloor}R,a:=a\bmod c$，然后递归，符号序列和原来一一对应。

如果 $a\lt c$，考虑交换 $x,y$ 轴使得 $a^{\prime}\ge c^{\prime}$，那么第 $k$ 个 $U$ 前有 $\left\lfloor\dfrac{kc-b-1}{a}\right\rfloor$ 个 $R$，那么由于要保证 $b^{\prime}\ge 0$，考虑去掉第一个 $U$ 即前面的部分，最后补上最后一个 $U$ 后面的部分，总的答案为：

$$ R^{\left\lfloor\dfrac{c-b-1}{a}\right\rfloor}\circ U\circ \operatorname{Solve}\left(n^{\prime}:=\left\lfloor\dfrac{na+b}{c}\right\rfloor-1,c^{\prime}:=a,a^{\prime}:=c,b^{\prime}:=c-b-1,U^{\prime}:=R,R^{\prime}:=U\right)\circ R^{n-\left\lfloor\dfrac{c\cdot \left\lfloor\frac{na+b}{c}\right\rfloor-b-1}{a}\right\rfloor} $$

复杂度 $\mathcal{O}\left(\log\max\left(a,c\right)\right)$ 如果单次乘法为 $\mathcal{O}\left(1\right)$

对于此题，构造列向量 $\left[\begin{matrix}\mathrm{cnt}_U\\\mathrm{cnt}_R\\\sum i\\\sum\left\lfloor\frac{ai+b}{c}\right\rfloor\\\sum\left\lfloor\frac{ai+b}{c}\right\rfloor^2\\\sum\left\lfloor\frac{ai+b}{c}\right\rfloor\cdot i\end{matrix}\right]$ 和对应的 $U,R$ 即可。

数学总结